A) Ratios:
Simplest form of expressing a fraction is referred to as ratios. A ratio is a comparison of the sizes of two or more quantities of the same kind by division. Assume a and b are two quantities of the same kind (same units), then the fraction a/b is called the ratio of a to b represented by a/b or a: b. ‘a’ is referred to as the antecedent and ‘b’ is referred to as the consequent.
Types of Ratios:
Assume two numbers a and b are in ratio a:b, then the different types of ratios are as follows:

General Note: In order to find a ratio from two numbers, eliminate the common factor. Similarly, to find the original numbers, multiply the ratio with the common factor.
Example: The two numbers 15 and 25 are in ratio, in order to find the simplest form of 15/ 25, we eliminate the common factor (i.e., dividing the numbers by 5). Hence the ratio is 3/5.
Similarly, we can find the original numbers by multiplying the ratio with common factor 5. (i.e., 3/5 *5/5)
B) Proportions:
An Equality of two ratios is called a proportion.
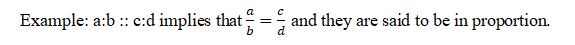
Notes:

Properties of Proportion: When two ratios are equal such that a/b = c/d then the following properties hold good:
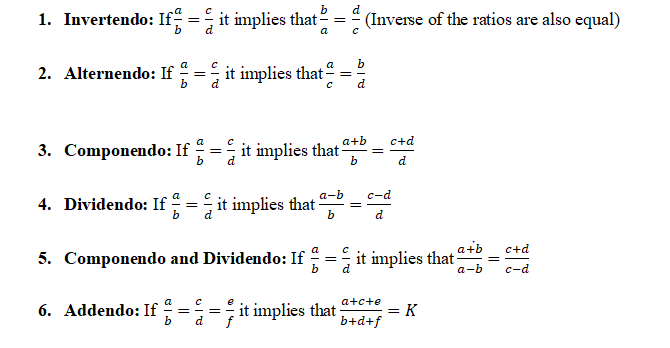
C) Indices:
Higher order arithmetic operations with powers and roots are referred to as Indices.
General Formulae:
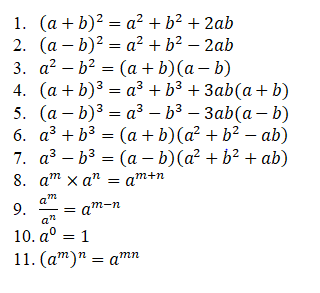
D) Logarithms:
Logarithms are used to simplify the calculations.
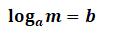
From the above ‘a’ is referred to as base, ‘b’ is referred to as power and ‘m’ is the number given.

Properties of Logarithms:

